X 36 plane Black & White Stock Photos
Evening Snow on the Asuka Mountain (Asukayama no Bosetsu) Utagawa Hiroshige (Ando) (Japanese, 1797-1858). Evening Snow on the Asuka Mountain (Asukayama no Bosetsu), ca. 1838. Color woodblock print on paper, Sheet: 9 3/16 x 14 1/2 in. (23.4 x 36.8 cm). To create the soft contours of the hillsides in this lovely rendering of the “snow in the evening” subject, Hiroshige’s printer employed a technique called bokashi. Unlike most woodblock printing, in which ink is applied evenly across the block for a consistent plane of color, for this technique the printer uses moisture and smears to create gra Stock Photohttps://www.alamy.com/image-license-details/?v=1https://www.alamy.com/evening-snow-on-the-asuka-mountain-asukayama-no-bosetsu-utagawa-hiroshige-ando-japanese-1797-1858-evening-snow-on-the-asuka-mountain-asukayama-no-bosetsu-ca-1838-color-woodblock-print-on-paper-sheet-9-316-x-14-12-in-234-x-368-cm-to-create-the-soft-contours-of-the-hillsides-in-this-lovely-rendering-of-the-snow-in-the-evening-subject-hiroshiges-printer-employed-a-technique-called-bokashi-unlike-most-woodblock-printing-in-which-ink-is-applied-evenly-across-the-block-for-a-consistent-plane-of-color-for-this-technique-the-printer-uses-moisture-and-smears-to-create-gra-image504699437.htmlRM2M9317W–Evening Snow on the Asuka Mountain (Asukayama no Bosetsu) Utagawa Hiroshige (Ando) (Japanese, 1797-1858). Evening Snow on the Asuka Mountain (Asukayama no Bosetsu), ca. 1838. Color woodblock print on paper, Sheet: 9 3/16 x 14 1/2 in. (23.4 x 36.8 cm). To create the soft contours of the hillsides in this lovely rendering of the “snow in the evening” subject, Hiroshige’s printer employed a technique called bokashi. Unlike most woodblock printing, in which ink is applied evenly across the block for a consistent plane of color, for this technique the printer uses moisture and smears to create gra
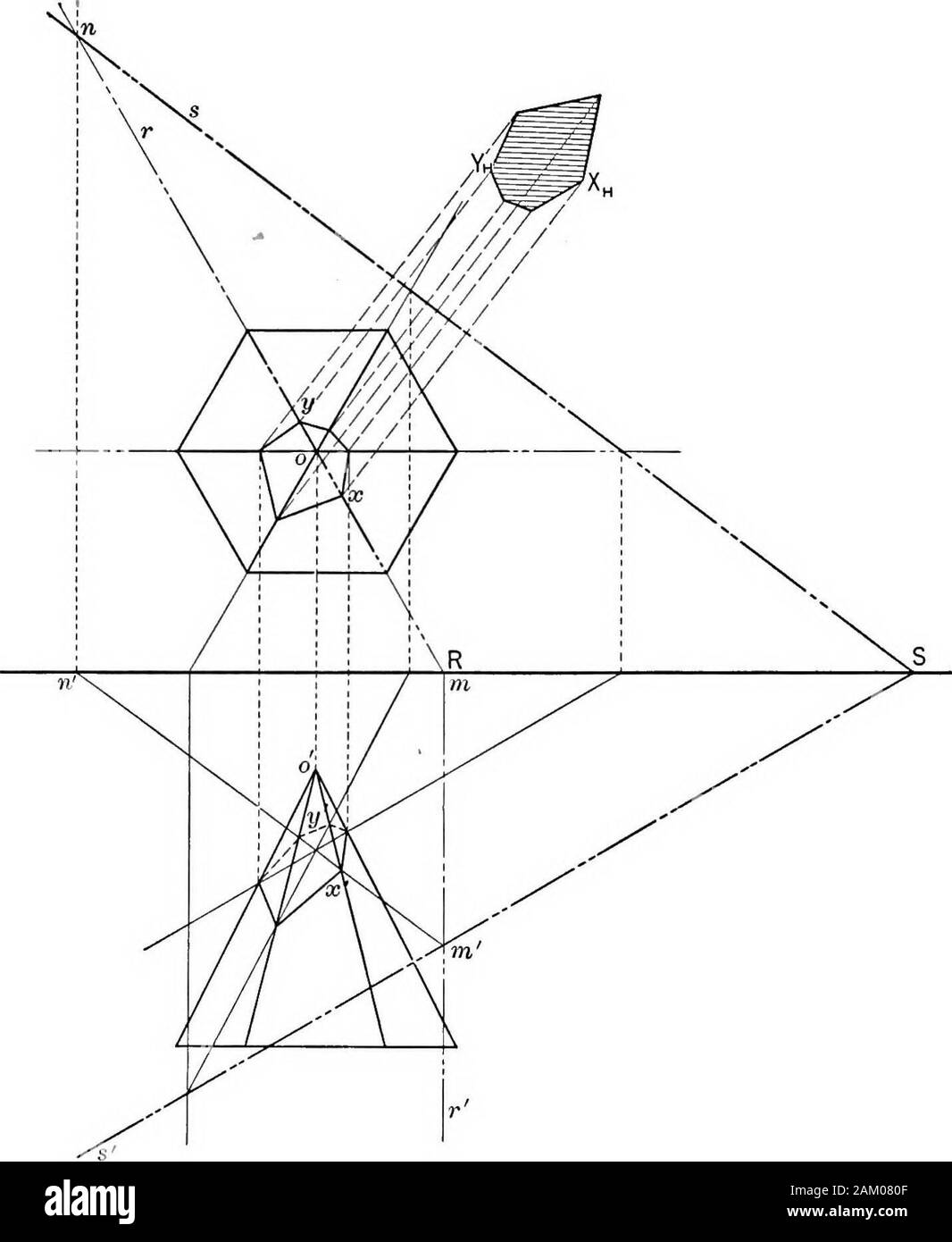The essentials of descriptive geometry . Fig. 76. Construction. In Fig. 77, 0 is the apex of a solid octagonalpyramid whose base is in a plane parallel to H. By Article 56find where each edge pierces the cutting plane S, as at X, Y, etc.Join these points in order and the area thus enclosed will be thesection cut from the surface by the plane S. If the true size of 96 ESSENTIALS OF DESCRIPTIVE GEOMETRY the section is required it may be found by revolving it into H orV. In this figure the section is revolved into H about the tracesS (Article 36), and its true ^ size is shown by the hatched areaa Stock Photohttps://www.alamy.com/image-license-details/?v=1https://www.alamy.com/the-essentials-of-descriptive-geometry-fig-76-construction-in-fig-77-0-is-the-apex-of-a-solid-octagonalpyramid-whose-base-is-in-a-plane-parallel-to-h-by-article-56find-where-each-edge-pierces-the-cutting-plane-s-as-at-x-y-etcjoin-these-points-in-order-and-the-area-thus-enclosed-will-be-thesection-cut-from-the-surface-by-the-plane-s-if-the-true-size-of-96-essentials-of-descriptive-geometry-the-section-is-required-it-may-be-found-by-revolving-it-into-h-orv-in-this-figure-the-section-is-revolved-into-h-about-the-tracess-article-36-and-its-true-size-is-shown-by-the-hatched-areaa-image339296399.htmlRM2AM080F–The essentials of descriptive geometry . Fig. 76. Construction. In Fig. 77, 0 is the apex of a solid octagonalpyramid whose base is in a plane parallel to H. By Article 56find where each edge pierces the cutting plane S, as at X, Y, etc.Join these points in order and the area thus enclosed will be thesection cut from the surface by the plane S. If the true size of 96 ESSENTIALS OF DESCRIPTIVE GEOMETRY the section is required it may be found by revolving it into H orV. In this figure the section is revolved into H about the tracesS (Article 36), and its true ^ size is shown by the hatched areaa
